Imaginary Numbers, Real Belonging
Dr. Stephanie Edwards
In many ways, mathematics is art — at least for Dr. Stephanie Edwards. She’s always had an affinity for the field, but it really blossomed when she was in graduate school. Doing complex analysis (math beyond calculus) brought home to her that math is beautiful — and it works.
Complex analysis is, as the name suggests, complicated. “The easy way to see it is calculus with imaginary numbers thrown in,” Edwards says. Imaginary numbers are created possibilities from mathematical impossibilities. “What’s the square root of negative one?” Edwards asks. Logically, it’s an impossible question: two negatives multiplied together yield a positive — there’s nothing that, multiplied by itself, will result in a negative real number. However, mathematicians “imagined what would happen if you could” multiply a number by itself to arrive at negative one, Edwards says. That something is an imaginary number, .
Like a child’s imagination, these fictitious numbers “open a whole new world, and you can take problems — real world problems — and solve them in the complex plane,” Edwards says. Then the answers can be applied to the real world, thereby solving real problems. Any type of fluid flow — how water moves around rocks in a river, how air moves around the wings of an airplane, how boats move through water — is part of complex analysis. You will see it applied to electronics, circuits, amplifiers, and in general oscillating systems. (Hope’s engineering and physics departments love it when their majors have taken complex analysis, Edwards says, because it opens up so many ways for them to solve problems.)
Edwards’ research stays within her “Mathematical Family.” Her advisor’s advisor’s advisor was the well-known mathematician, educator and problem solver George Pólya. She and her mathematical siblings have all studied his work. Most of his results require functions to have only “real zeros.”
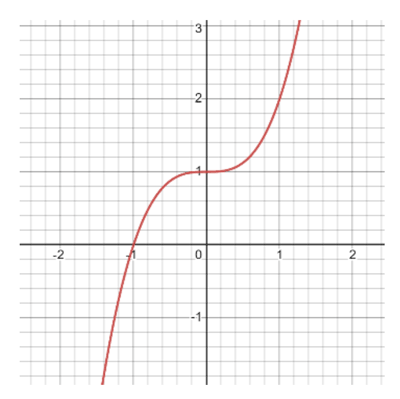
In a polynomial equation such as y = x³ + 1, a zero is the value of x when y is equal to zero. One can think of it as where the graph of the function crosses the x-axis. Complex or “nonreal” zeros are solutions that can’t be represented on a graph. In the example above, the real zero is at -1 and the nonreal zeros are at .
“For my research, I take Pólya’s theorems, and I’ll say: ‘What happens if we relax the hypothesis and allow functions that have nonreal zeros?’” Edwards says. “Where does his argument fail? Pólya was a really smart guy; in general, his argument won’t work for functions with nonreal zeros, so we use technology to give us insight into ways to prove (or disprove) new results.” Edwards’ students have presented their work at regional and national meetings. Some have even won awards for their presentations on the research.
Edwards has experienced challenges beyond those in mathematics. She found herself battling a rare form of cancer, Ewing’s sarcoma, and during her year of chemotherapy she was on medical leave. During the time of healing and reflection, she concentrated on what brought her joy. When she finally returned to work, she told her students, “I’m exhausted, but you bring me such joy being in this classroom.”
One of her greatest joys is witnessing her students experience “math moments.” A “math moment” is that time of enlightenment, excitement, and clarity when a person finally makes a connection within the material that leads to understanding. The environment must be encouraging for students to be able to have such a moment. “A lot of it is making them feel valued as people. They may not understand a specific concept; it doesn’t mean they can’t understand it,” she says. “And any time a student has a math moment, the whole class will celebrate.”
In Edwards’ experience, math moments abound at conferences. She’s currently the president of Pi Mu Epsilon, the national honorary mathematics society. It’s a volunteer-run organization whose funds go directly to students “to promote the joy of mathematics,” Edwards says, often by sending them to conferences to present their work and hear about work by others. Pi Mu Epsilon is organizing most of the undergraduate content for the January 2023 Joint Mathematics Meetings (the largest annual gathering of mathematicians in the world). Edwards will be traveling to Boston with ten Hope students, some of whom will present their research. The entire group will be learning all that the mathematical community can offer them. “Students can go and see: There are people who love to do the same things you do, and they’re cool. They’re not dorky,” Edwards says. “Mathematics is community. I guess my whole life’s about community, because working in a group where you feel accepted and valued can make such a difference.”
That community is something Edwards especially hopes to bring to the forefront for female students, who are in the minority in a largely male-dominated field. She regularly brings students to the Nebraska Conference for Undergraduate Women in Mathematics, which she sees as a foundational experience.
“They come back feeling inspired and that they can do things,” she says. “That’s the big thing. They don’t have to go into math. They don’t have to go to graduate school. They just have to know they can do it, and that it changes the world.”
Edwards has introduced innovative projects to bring community onto the Hope campus, too. Among her fondest achievements is her button project. Students are given buttons with mathematical symbols directly tied to the class they are taking. The students then pin them to their backpacks. Now, Edwards says, “you walk around campus and you see students with one or two buttons, but then you see some with a whole billboard, like I have, and they get so excited about it. It’s something little that can create solidarity. Mathematics is so much thought of as an isolated field, so any way you can start making people feel belonging makes a big difference.”
Battling the perception that math is isolated — even isolating — is key to Edwards’ mentorship philosophy. “Interdisciplinary stuff: that’s where everything’s at — bringing ideas from different places, learning something else and making progress. And you can’t do that in an isolated environment,” she says. Edwards invites new math majors to stop by her office to personally receive a book of short stories of triumphs in math, and the message behind them: “Math is hard, but you can do it.” Department social events often feature strategy games that apply mathematical thinking to a more casual realm, such as backgammon or Settlers of Catan.
Visitors to the Department of Mathematics and Statistics in VanderWerf Hall may see another of Edwards’ initiatives: the “VanderBoards.” Two enormous outdoor chalkboards serve as a community forum. Whenever a new problem’s added, people can gather informally to discuss solutions, or set them down in chalk — Good Will Hunting style.
“Mathematics is community. I guess my whole life’s about community, because working in a group where you feel accepted and valued can make such a difference.”
Edwards’ calculus classes are treated to trips to Hope’s Kruizenga Art Museum, where they hear about art creation and apply it to mathematics. “You can put different parts together and sometimes it doesn’t fit well,” Edwards explains. “Sometimes you start out with a block and you subtract to get to your art,” as with a marble sculpture. “Sometimes you add to get your art,” as with a clay one. “I’d have students write a reflective paper on how mathematics is the same way.” They take measurements of an ancient ornate bell too large to practically weigh and a sugar bowl too delicate to fill, using calculus and mathematical modeling to estimate their weights and volumes.
Edwards credits the success of such initiatives to the dynamics at Hope, and specifically her department. “The community in our department, it’s different,” she says. “The people make all the difference in the world.”